Dynamic analysis of a beam
We perform the dynamic analysis of a steel catenary riser (SCR) subject to forced top motions. We compare the results against the corresponding SIMA/RIFLEX example case. The riser consists of three segments with two different cross-sections.
using Muscade, StaticArrays, GLMakie, Muscade.Toolbox, Interpolations, CSV, DataFramesRead RIFLEX motions, tensions, bending moment and curvatures time series (verification data)
file_path = "SCR.csv"
df = CSV.read(file_path, DataFrame; delim=' ')
dynMotionX = vcat(0,df[:,"Displacement in x - direction"].-df[1,"Displacement in x - direction"],df[end,"Displacement in x - direction"]-df[1,"Displacement in x - direction"])
dynMotionZ = vcat(0,df[:,"Displacement in z - direction"].-df[1,"Displacement in z - direction"],df[end,"Displacement in z - direction"]-df[1,"Displacement in z - direction"])
dynMotionT = vcat(-10.,df[:,"x"],df[end,"x"]+100)
xMotion = linear_interpolation(dynMotionT,-dynMotionX)
zMotion = linear_interpolation(dynMotionT,dynMotionZ);Some physical constants
const g=9.81
const ρ=1025.;Define parameters for cross-section 1
x1_D = 0.429 # Outer diameter [m]
x1_t = 0.022 # Thickness [m]
x1_steelArea = (x1_D-x1_t)*π*x1_t # Pipe wall area [m^2]
x1_innerArea = (x1_D-2*x1_t)^2*π/4 # Inner area [m^2]
x1_ρₛ = 7850. # Steel denstiy [kg/m^3]
x1_ρᵢ = 200. # Internal fluid density [kg/m^3]
x1_EA = 5.823e9 # Axial stiffness [N]
x1_EI₂ = 1.209e8 # Bending stiffness [Nm/(1/m)]
x1_EI₃ = 1.209e8 # Bending stiffness [Nm/(1/m)]
x1_GJ = 9.347e7 # Torsional stiffness [Nm/(rad/m)]
x1_μ = x1_steelArea*x1_ρₛ + x1_innerArea*x1_ρᵢ # Mass per unit length [m]
x1_ι₁ = 0.2053^2*x1_steelArea*x1_ρₛ # Moment of inertia about x-axis per unit length [kgm²/m]
x1_w = x1_μ*g - π*x1_D^2/4*ρ*g # Weight per unit length [N/m]
x1_Dh = 0.459 # Hydrodynamic outer diameter [m]
x1_Ca₂ = 1.0 * ρ * π*x1_Dh^2/4 # Transverse added mass coefficients [N/m/(m/s^2)]
x1_Ca₃ = 1.0 * ρ * π*x1_Dh^2/4
x1_Cq₂ = 1.0 * 0.5 * ρ * x1_Dh # Transverse drag coefficients [N/m/(m/s)^2]
x1_Cq₃ = 1.0 * 0.5 * ρ * x1_Dh
x1_mat = BeamCrossSection(EA=x1_EA, EI₂=x1_EI₂, EI₃=x1_EI₃, GJ=x1_GJ, μ=x1_μ, ι₁=x1_ι₁, Ca₂=x1_Ca₂, Cq₂=x1_Cq₂, Ca₃=x1_Ca₃, Cq₃=x1_Cq₃)BeamCrossSection(5.823e9, 1.209e8, 1.209e8, 9.347e7, 244.10222042282496, 9.307102957808986, 0.0, 0.0, 0.0, 0.0, 169.60518222430625, 0.0, 235.2375, 169.60518222430625, 0.0, 235.2375)Define parameters for cross-section 2
x2_D = 0.441 # Outer diameter [m]
x2_t = 0.028 # Thickness [m]
x2_steelArea = (x2_D-x2_t)*π*x2_t # Pipe wall area [m^2]
x2_innerArea = (x2_D-2*x2_t)^2*π/4 # Inner area [m^2]
x2_ρₛ = 7850. # Steel denstiy [kg/m^3]
x2_ρᵢ = 200. # Internal fluid density [kg/m^3]
x2_EA = 7.520e9 # Axial stiffness [N]
x2_EI₂ = 1.611e8 # Bending stiffness [Nm/(1/m)]
x2_EI₃ = 1.611e8 # Bending stiffness [Nm/(1/m)]
x2_GJ = 1.245e8 # Torsional stiffness [Nm/(rad/m)]
x2_μ = x2_steelArea*x2_ρₛ + x2_innerArea*x2_ρᵢ # Mass per unit length [m]
x2_ι₁ = 0.2084^2*x2_steelArea*x2_ρₛ # Moment of inertia about x-axis per unit length [kgm²/m]
x2_w = x2_μ*g - π*x2_D^2/4*ρ*g # Weight per unit length [N/m]
x2_Dh = 0.471 # Hydrodynamic outer diameter [m]
x2_Ca₂ = 1.0 * ρ * π*x2_Dh^2/4 # Transverse added mass coefficients [N/m/(m/s^2)]
x2_Ca₃ = 1.0 * ρ * π*x2_Dh^2/4
x2_Cq₂ = 1.0 * 0.5 * ρ * x2_Dh # Transverse drag coefficients [N/m/(m/s)^2]
x2_Cq₃ = 1.0 * 0.5 * ρ * x2_Dh
x2_mat = BeamCrossSection(EA=x2_EA, EI₂=x2_EI₂, EI₃=x2_EI₃, GJ=x2_GJ, μ=x2_μ, ι₁=x2_ι₁, Ca₂=x2_Ca₂, Cq₂=x2_Cq₂, Ca₃=x2_Ca₃, Cq₃=x2_Cq₃)BeamCrossSection(7.52e9, 1.611e8, 1.611e8, 1.245e8, 308.46874150589946, 12.385770874447834, 0.0, 0.0, 0.0, 0.0, 178.58935181540963, 0.0, 241.3875, 178.58935181540963, 0.0, 241.3875)Model SCR, starting from the extremity located on seabed
nel = [60, 30, 10] # Number of elements per segment
segLength = [300., 300., 80.] # Segment lengths
xSection = [x1_mat, x2_mat, x1_mat]; # Cross-section typeFor each segment, build a vector of (matrices describing node coordinates)
nseg = length(nel)
accLength = [0;cumsum(segLength)]
nnodes = nel.+1
nodeCoord = [
hcat( accLength[seg] .+ ((1:nnodes[seg]).-1)/(nnodes[seg]-1)*segLength[seg],
0 .+ zeros(Float64,nnodes[seg],1),
-300 .+ zeros(Float64,nnodes[seg],1)) for seg=1:nseg
];Create Muscade model
model = Model(:CatenaryRiser);Lists with First and last node of each segment, etc.
firstNode = Vector{Muscade.NodID}(undef,nseg)
lastNode = Vector{Muscade.NodID}(undef,nseg)
nodeList = Vector{Vector{Muscade.NodID}}(undef,nseg)
global elementList = Vector{Muscade.EleID};Populate lists for Segment 1
nodid = addnode!(model,nodeCoord[1])
mesh = hcat(nodid[1:nnodes[1]-1],nodid[2:nnodes[1]])
elementList = addelement!(model,EulerBeam3D,mesh;mat=xSection[1],orient2=SVector(0.,1.,0.))
firstNode[1] = nodid[1]
lastNode[1] = nodid[size(nodid,1)]
nodeList[1] = nodid;Populate list for the other segments
if nseg>=2
for segid ∈ 2:nseg
local nodid = addnode!(model,nodeCoord[segid][2:end,:])
firstNode[segid] = lastNode[segid-1]
lastNode[segid] = nodid[size(nodid,1)]
local mesh = hcat(nodid[1:(nnodes[segid]-2)],nodid[2:(nnodes[segid]-1)])
global elementList=vcat(elementList,addelement!(model,EulerBeam3D,[firstNode[segid],nodid[1]]; mat=xSection[segid],orient2=SVector(0.,1.,0.)))
global elementList=vcat(elementList,addelement!(model,EulerBeam3D,mesh; mat=xSection[segid],orient2=SVector(0.,1.,0.)))
nodeList[segid] = nodid
end
endFix lower extremity
[addelement!(model,Hold,[firstNode[1]] ;field) for field∈[:t1,:t2,:t3,:r1]];Loading procedure for the static analysis is as follows
- start by elongating the line to create geometric stiffness
- apply the weight (can be done rapidly)
- move the end of the line to the prescribed displacement
- contact forces
Define the prescribed end displacements of the top extremity
@functor with(xMotion) horizMove(x,t)=x[1] - (1.0 - exp(minimum([t,0]))*(181.0) + xMotion(t))
@functor with(zMotion) vertMove(x,t)= x[1] - (exp(minimum([t,0]))*303.1 + zMotion(t))
addelement!(model,DofConstraint,[lastNode[3]],xinod=(1,),xfield=(:t1,), λinod=1, λclass=:X, λfield=:λt1, gap=horizMove, mode=equal)
addelement!(model,DofConstraint,[lastNode[3]],xinod=(1,),xfield=(:t3,), λinod=1, λclass=:X, λfield=:λt3, gap=vertMove, mode=equal);Define the loading procedure for the weight (this should eventually be transfered to the element, involving the definition a tunable gravity field, work in progress)
@functor with(x1_w,segLength,nel) weight1(t) = - ((min(t,-5.)+10)/5) * x1_w * segLength[1] / nel[1];
@functor with(x2_w,segLength,nel) weight2(t) = - ((min(t,-5.)+10)/5) * x2_w * segLength[2] / nel[2];
@functor with(x1_w,segLength,nel) weight3(t) = - ((min(t,-5.)+10)/5) * x1_w * segLength[3] / nel[3];
for idxNod = 1:length(nodeList[1])
addelement!(model,DofLoad,[nodeList[1][idxNod]];field=:t3,value=weight1);
end
for idxNod = 1:length(nodeList[2])
addelement!(model,DofLoad,[nodeList[2][idxNod]];field=:t3,value=weight2);
end
for idxNod = 1:length(nodeList[3])
addelement!(model,DofLoad,[nodeList[3][idxNod]];field=:t3,value=weight3);
end
for idxNod = 1:length(nodeList[1])
addelement!(model,SoilContact,[nodeList[1][idxNod]],z₀=0.,Kh=1.0e3,Kv=1.0e4,Ch=0.,Cv=0.);
endRun the static analysis
initialstate = initialize!(model);
staticLoadSteps = (-10:.2:0)*1.
nStaticLoadSteps = length(staticLoadSteps)
staticStates = solve(SweepX{0};initialstate,time=staticLoadSteps,verbose=true,maxΔx=1e-6,maxiter=100);
Muscade: SweepX{0} solver
step 1 converged in 4 iterations. |Δx|=5.6e-08 |Lλ|=1.0e-05
step 2 converged in 5 iterations. |Δx|=1.2e-08 |Lλ|=1.6e-05
step 3 converged in 4 iterations. |Δx|=6.4e-08 |Lλ|=1.8e-05
step 4 converged in 4 iterations. |Δx|=1.8e-07 |Lλ|=1.9e-05
step 5 converged in 4 iterations. |Δx|=6.9e-08 |Lλ|=1.8e-05
step 6 converged in 4 iterations. |Δx|=1.7e-07 |Lλ|=1.7e-05
step 7 converged in 4 iterations. |Δx|=3.2e-07 |Lλ|=1.9e-05
step 8 converged in 4 iterations. |Δx|=9.2e-08 |Lλ|=1.8e-05
step 9 converged in 4 iterations. |Δx|=1.3e-07 |Lλ|=1.8e-05
step 10 converged in 4 iterations. |Δx|=3.3e-07 |Lλ|=1.9e-05
step 11 converged in 4 iterations. |Δx|=1.8e-07 |Lλ|=1.7e-05
step 12 converged in 4 iterations. |Δx|=2.2e-07 |Lλ|=1.6e-05
step 13 converged in 4 iterations. |Δx|=2.3e-07 |Lλ|=1.6e-05
step 14 converged in 4 iterations. |Δx|=8.6e-08 |Lλ|=2.1e-05
step 15 converged in 4 iterations. |Δx|=2.2e-07 |Lλ|=1.6e-05
step 16 converged in 4 iterations. |Δx|=4.5e-07 |Lλ|=1.7e-05
step 17 converged in 5 iterations. |Δx|=1.0e-07 |Lλ|=1.7e-05
step 18 converged in 5 iterations. |Δx|=1.6e-07 |Lλ|=1.4e-05
step 19 converged in 5 iterations. |Δx|=5.9e-08 |Lλ|=1.4e-05
step 20 converged in 5 iterations. |Δx|=4.6e-08 |Lλ|=1.7e-05
step 21 converged in 5 iterations. |Δx|=9.7e-09 |Lλ|=1.5e-05
step 22 converged in 5 iterations. |Δx|=5.7e-08 |Lλ|=1.8e-05
step 23 converged in 5 iterations. |Δx|=1.6e-07 |Lλ|=1.9e-05
step 24 converged in 5 iterations. |Δx|=8.9e-08 |Lλ|=2.0e-05
step 25 converged in 5 iterations. |Δx|=8.1e-08 |Lλ|=1.5e-05
step 26 converged in 5 iterations. |Δx|=3.7e-08 |Lλ|=2.0e-05
step 27 converged in 5 iterations. |Δx|=5.0e-07 |Lλ|=1.9e-05
step 28 converged in 6 iterations. |Δx|=1.7e-08 |Lλ|=1.8e-05
step 29 converged in 6 iterations. |Δx|=2.3e-08 |Lλ|=1.5e-05
step 30 converged in 6 iterations. |Δx|=8.9e-09 |Lλ|=2.1e-05
step 31 converged in 6 iterations. |Δx|=5.0e-09 |Lλ|=1.4e-05
step 32 converged in 6 iterations. |Δx|=4.0e-09 |Lλ|=2.0e-05
step 33 converged in 6 iterations. |Δx|=3.8e-10 |Lλ|=1.8e-05
step 34 converged in 6 iterations. |Δx|=5.9e-10 |Lλ|=1.8e-05
step 35 converged in 6 iterations. |Δx|=3.5e-09 |Lλ|=1.7e-05
step 36 converged in 6 iterations. |Δx|=1.7e-08 |Lλ|=2.2e-05
step 37 converged in 6 iterations. |Δx|=1.1e-07 |Lλ|=9.7e-05
step 38 converged in 6 iterations. |Δx|=6.9e-07 |Lλ|=6.8e-04
step 39 converged in 7 iterations. |Δx|=3.0e-10 |Lλ|=2.2e-05
step 40 converged in 7 iterations. |Δx|=3.9e-10 |Lλ|=2.3e-05
step 41 converged in 7 iterations. |Δx|=1.7e-10 |Lλ|=2.2e-05
step 42 converged in 7 iterations. |Δx|=2.4e-09 |Lλ|=2.4e-05
step 43 converged in 7 iterations. |Δx|=1.4e-07 |Lλ|=4.3e-05
step 44 converged in 8 iterations. |Δx|=5.5e-10 |Lλ|=3.0e-05
step 45 converged in 8 iterations. |Δx|=6.6e-09 |Lλ|=4.5e-05
step 46 converged in 9 iterations. |Δx|=5.6e-11 |Lλ|=2.8e-05
step 47 converged in 9 iterations. |Δx|=2.2e-10 |Lλ|=6.2e-05
step 48 converged in 9 iterations. |Δx|=5.6e-10 |Lλ|=8.5e-05
step 49 converged in 10 iterations. |Δx|=1.9e-10 |Lλ|=1.3e-04
step 50 converged in 10 iterations. |Δx|=6.3e-07 |Lλ|=1.6e-03
step 51 converged in 12 iterations. |Δx|=4.8e-09 |Lλ|=2.1e-04
nel=268, ndof=612, nstep=51, niter=296, niter/nstep= 5.80
SweepX{0} time: 15 [s]
Muscade done.Plot the static analysis sequence
fig = Figure(size = (1000,1000))
ax = Axis3(fig[1,1])
α = 2π*(0:19)/20
circle = 0.05*[cos.(α) sin.(α)]'
for stateIdx ∈ 1:nStaticLoadSteps
draw!(ax,staticStates[stateIdx],EulerBeam3D=(;style=:shape))
end
currentDir = @__DIR__
if occursin("build", currentDir)
save(normpath(joinpath(currentDir,"..","src","assets","staticEquilibriumSCR.png")),fig)
elseif occursin("examples", currentDir)
save(normpath(joinpath(currentDir,"staticEquilibriumSCR.png")),fig)
end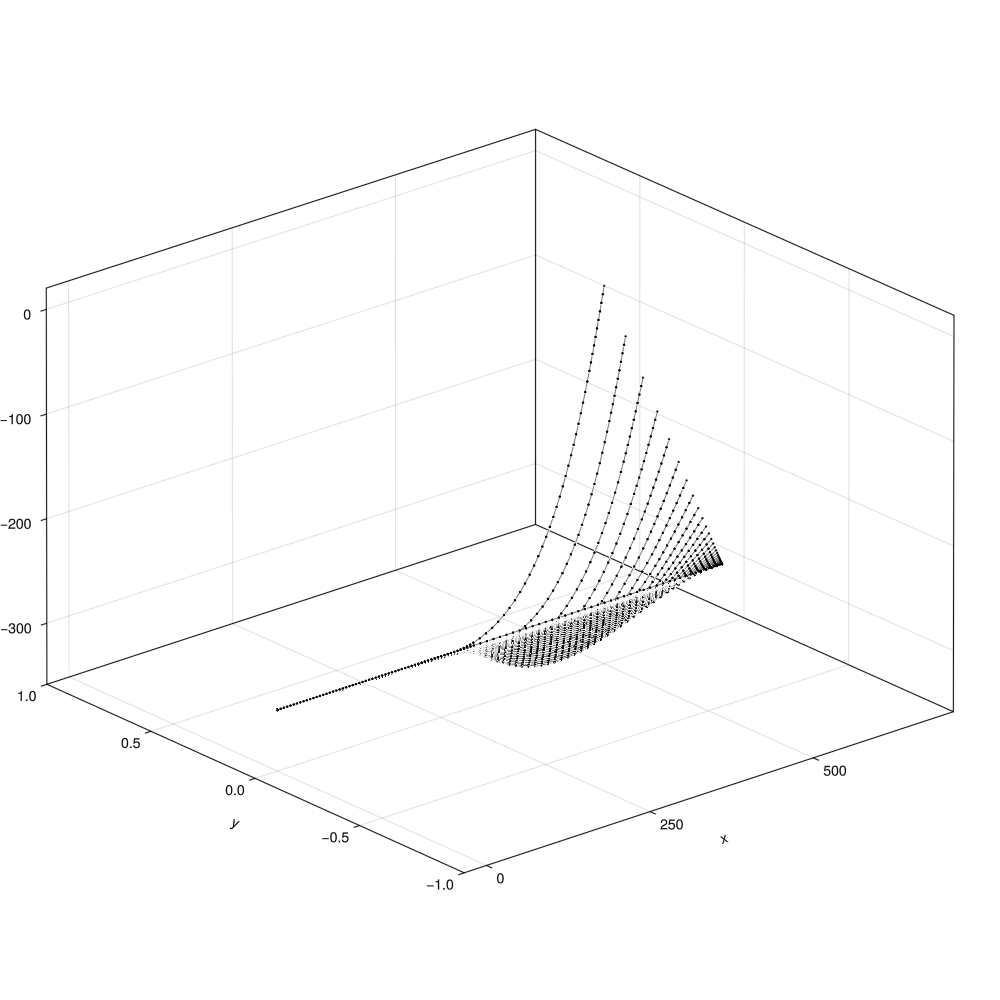
Run the dynamic analysis
dynamicLoadSteps = (0.1:0.3:300)*1.0
nDynamicLoadSteps = length(dynamicLoadSteps)
dynamicStates = solve(SweepX{2};
initialstate=staticStates[nStaticLoadSteps],
time=dynamicLoadSteps,
verbose=false,
maxΔx=1e-5);Retrieve axial force at top location
req = @request gp(resultants(fᵢ))
out = getresult(dynamicStates,req,[elementList[end]])
Fgp1_ = [ out[idxEl].gp[1][:resultants][:fᵢ] for idxEl ∈ 1:size(out,2)];Retrieve bending moments near touch down point
req = @request gp(resultants(mᵢ))
out = getresult(dynamicStates,req,[elementList[64]])
Mgp1_ = [ out[idxEl].gp[1][:resultants][:mᵢ] for idxEl ∈ 1:size(out,2)];Retrieve curvature near touch down point
req = @request gp(κgp)
out = getresult(dynamicStates,req,[elementList[64]])
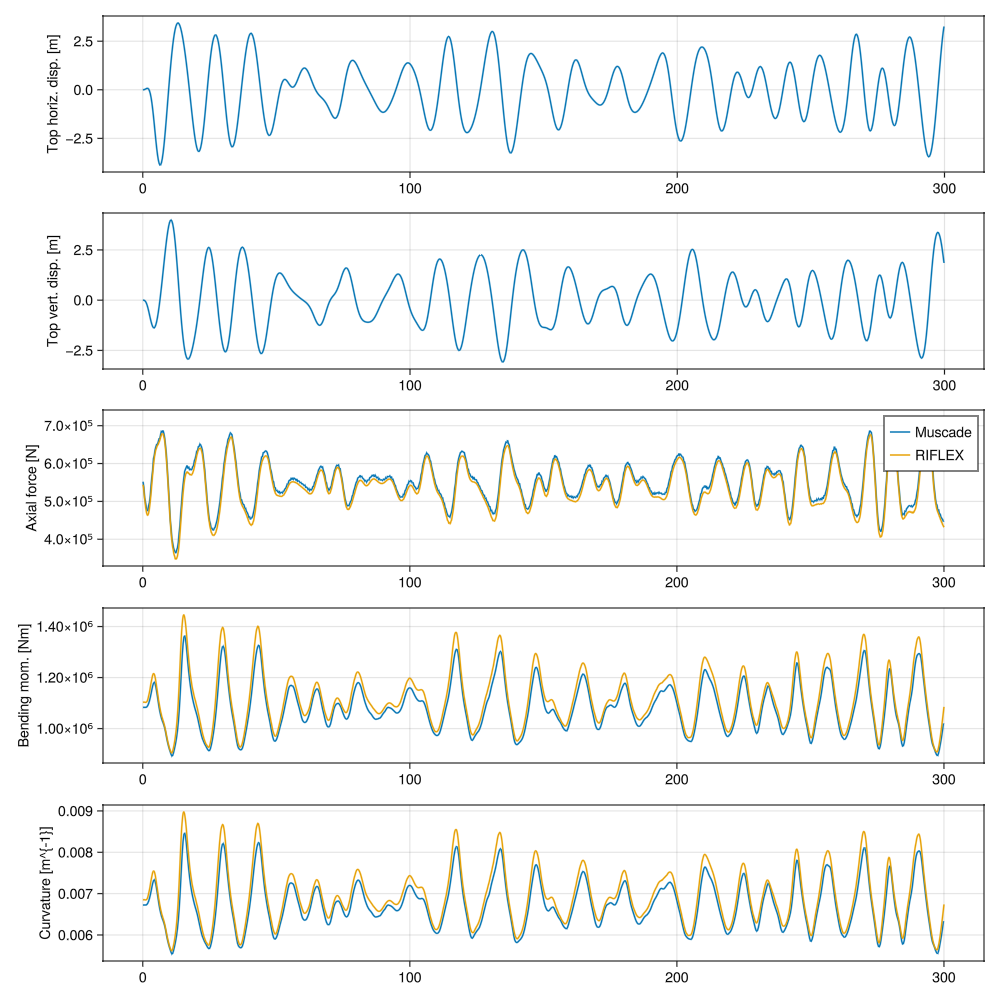
κgp1_ = [ out[idxEl].gp[1].κgp[1] for idxEl ∈ 1:size(out,2)];Plot comparison between Muscade and RIFLEX results.
fig2 = Figure(size = (1000,1000))
ax1 = Axis(fig2[1, 1],ylabel="Top horiz. disp. [m]")
lines!(ax1,dynamicLoadSteps,xMotion(dynamicLoadSteps))
ax2 = Axis(fig2[2, 1],ylabel="Top vert. disp. [m]")
lines!(ax2,dynamicLoadSteps,zMotion(dynamicLoadSteps))
ax3 = Axis(fig2[3, 1],ylabel="Axial force [N]")
lines!(ax3, dynamicLoadSteps, Fgp1_, label="Muscade")
lines!(ax3, df[:,"x"],df[:,"Axial force"], label="RIFLEX")
axislegend()
ax4 = Axis(fig2[4, 1],ylabel="Bending mom. [Nm]")
lines!(ax4, dynamicLoadSteps, getindex.(Mgp1_,3), label="Muscade")
lines!(ax4, df[:,"x"],df[:,"Mom. about local y-axis, end 1"], label="RIFLEX")
ax5 = Axis(fig2[5, 1],ylabel="Curvature [m^{-1}]")
lines!(ax5, dynamicLoadSteps, getindex.(κgp1_,3), label="Muscade")
lines!(ax5, df[:,"x"],df[:,"Curvature about local y-axis, end 1"], label="RIFLEX")
if occursin("build", currentDir)
save(normpath(joinpath(currentDir,"..","src","assets","dynamicAnalysisSCR.png")),fig2)
elseif occursin("examples", currentDir)
save(normpath(joinpath(currentDir,"dynamicAnalysisSCR.png")),fig2)
endMinor discrepancies might be due to the fact that loads are extracted at Gauss points in Muscade, while they are extracted at nodes in RIFLEX.
This page was generated using Literate.jl.